Космологическая модель с проективным мероопределением.

 

Приложение №1. Проективная космологическая модель и теория элементарных частиц.

В данном приложении намечены контуры теории элементарных частиц, основные постулаты которой совпадают с постулатами изложенной выше проективной космологической модели. Из всего множества проблем, которые должна разрешить теория элементарных частиц, здесь будут кратко рассмотрены только 2 проблемы:

1. единое описание всех известных 4-х взаимодействий;

2. единое описание происхождения всех фермионов;

1. Согласно изложенной выше космологической модели, «первичной реальностью» Вселенной является пространство скоростей СР³ вместе со своим абсолютом Q(СР³) и вещественным подпространством RP³. Если это действительно так, то причину всех взаимодействий следует искать именно во взаимоотношениях отдельных элементов проективного пространства скоростей и указанных подмножеств. Действительно, все известные 4 взаимодействия могут быть поставлены в соответствие  простейшим геометрическим структурам и инвариантам указанных 3-х пространств. Каждое взаимодействие отвечает определенной группе преобразований, которые оставляют неизменными абсолют пространства скоростей, проективные прямые, плоскости и сферы.

Для большей наглядности представим данное утверждение в виде таблицы:

 

Вид взаимодействия	Основной объект	Группа симметрии
Инерционно-гравитационное	Точка	S2×S2 (О(4,С))
Электро-магнитное	Прямая	СP1 (О(3,С)); RP1 (U(1))
Сильное	Плоскость	RP2  (SU(3)/Z2)
Слабое	Сфера	S3  (SU(2))

 

Рассмотрим каждое из взаимодействий более подробно

1.1. Гравитационное взаимодействие.

В стандартной теории гравитационное взаимодействие рассматривается как искривление псевдоевклидового пространства-времени. Проективная космологическая модель указывает причину, вследствие которой метрика пространства-времени является псевдоевклидовой. Однако в рамках изложенной модели может быть построена еще одна модель гравитационного взаимодействия, которая в общих чертах сводится к следующему.

Для любой пары частиц, расположенных внутри абсолюта, может быть введен проективный инвариант – двойное отношение. Это отношение определяется четырьмя точками: две точки представляют положение данных частиц, а еще две точки – это точки пересечения с абсолютом прямой, соединяющей первые две точки. Логарифм двойного отношения представляет собой расстояние между точками, а квадрат этого расстояния может быть отождествлен с гравитационным потенциалом.

 

рис. 2.

 

Возникновение данного потенциала может быть представлено, как натяжение соединяющей частицы прямой, а само натяжение осуществляется абсолютом пространства скоростей. Указанные прямые соединяют данную частицу со всеми остальными частицами, и суммарная величина натяжений создает внутреннюю энергию частицы, которая с точностью до постоянного коэффициента, равного квадрату предельной скорости, совпадает с инертной массой частицы.

Таким образом, в рамках данной модели пропорциональность инертной и гравитационной массы объясняется тем, что обе массы имеют в своей основе одну и ту же причину – абсолют пространства скоростей.  Вполне возможно, что объединение данного механизма возникновения массы с изложенной в следующем разделе моделью возникновения известных типов элементарных частиц, позволит получить наблюдаемый спектр масс всех элементарных частиц.

1.2. Электромагнитное взаимодействие.

В наиболее общей формулировке уравнений Максвелла, в которой все 4 уравнения сводятся к одному уравнению, векторы электрического и магнитного полей образуют единый вектор в 3-х мерном комплексном пространстве, а группа Лоренца является группой вращений О(3,С) этого пространства ([3] стр.186). С другой стороны, группа О(3,С) изоморфна группе SL(2), которая изоморфна группе преобразований комплексной проективной прямой CP¹  ([2] стр.319). Как было указано выше, комплексная проективная прямая CP¹ есть не что иное, как ориентированная сфера S². В итоге, находим, что группа симметрии электромагнитного взаимодействия изоморфна группе симметрии ориентированной сферы S², т.е. той части абсолюта, которая попадает внутрь действительного пространства скоростей.

Градиентная инвариантность уравнений Максвелла является следствием еще одного изоморфизма группы О(3,С). В соответствие с так называемым «перенесением Плюккера», данная группа изоморфна группе преобразований геометрии прямых 3-х мерного действительного проективного пространства ([2] стр.319). Наглядно возможность описания электромагнетизма с помощью геометрии прямых в проективном пространстве продемонстрирована в ([1] стр.349), где плюккеровы координаты проективной прямой представлены как элементы кососимметрической матрицы 4-ого ранга. Тензор электромагнитного поля и представляет собой кососимметрический тензор 4-ого ранга. Группа преобразований действительной проективной прямой RP¹ изоморфна группе U(1). Инвариантность относительно этой группы и составляет наиболее общее выражение градиентной инвариантности.

Таким образом, наряду с полевым описанием, электромагнитные явления допускают проективное описание, в котором взаимодействие частиц осуществляется посредством проективных прямых. Эти прямые можно рассматривать как силовые линии, направленные либо от заряда (если заряд положительный), либо к заряду (если заряд отрицательный). В любой конечной области пространства эти силовые линии совпадают с обычными силовыми линиями в евклидовом пространстве. Отличие заключается  лишь в поведении силовых линий «на бесконечности», где обычные силовые линии пропадают, а проективные силовые линии замыкаются.

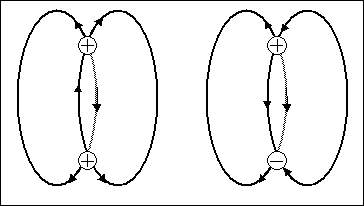
Величина натяжения проективных силовых линий определяется величиной электрического заряда и в зависимости от знака заряда это натяжение направлено либо от заряда (положительный заряд), либо – к заряду (отрицательный заряд). Взаимодействие зарядов представляет собой наложение проективных силовых линий. Результат такого наложения для одноименных и противоположных зарядов показан на рисунке 3.

 

Рис.3

 

При взаимодействии одноименных зарядов натяжения участков проективных силовых линий на отрезке, соединяющей эти заряды прямой, направлены в противоположные стороны и взаимно компенсируют друг друга (рис. 3а). В то же время, натяжение участков проективных силовых линий, проходящих через бесконечность, усиливают друг друга, что и приводит к отталкиванию зарядов (фактически, заряды отталкиваются за счет натяжения участков силовых линий, проходящих через бесконечность).

В случае противоположных зарядов происходит компенсирование натяжения участков силовых линий, проходящих через бесконечность, а натяжение участков силовых линий, расположенных между зарядами в конечной области пространства усиливают друг друга, благодаря чему и происходит притяжение зарядов (рис. 3б).

Описание взаимодействия зарядов посредством проективных силовых линий представляется более отвечающим действительности, чем посредством «виртуальных фотонов».

Еще одним достоинством предложенной картины взаимодействия электрических зарядов с помощью проективных силовых линий является то, она позволяет наиболее просто получить функциональную зависимость потенциала взаимодействия зарядов от расстояния. Величина натяжения проективной силовой линии имеет одно и то же значение как вблизи заряда, так и на сколь угодно большом расстоянии от него. Это означает, что создаваемый элементарным зарядом потенциал натяжения должен изменяться обратно пропорционально расстоянию от заряда. Соответственно, сила взаимодействия, как градиент потенциала, должна убывать обратно пропорционально квадрату расстояния.

1.3. Сильное взаимодействие.

Согласно предлагаемой модели, группа симметрии сильных взаимодействий тождественна группе преобразований вещественной проективной плоскости RР². Эта группа имеет вид:

 

ρХ₁' = а₁₁ Х₁ + а₁₂ Х₂ + а₁₃ Х₃

                ρХ₂' = а₂₁ Х₁ + а₂₂ Х₂ + а₂₃ Х₃                 (7)        

ρХ₃' = а₃₁ Х₁ + а₃₂ Х₂ + а₃₃ Х₃

 

Данная группа имеет такое же число независимых параметров n = (9-1) = 8, как и группа SU(3). Это позволяет предположить, что с помощью группы RР²  сильное взаимодействие может быть описано не менее успешно, чем с помощью группы SU(3).

В известной автору математической литературе не указано детальное соотношение между группами RР² и SU(3). По-видимому, это соотношение такое же, как между группами RР³  и группой SU(2), т.е. группа SU(3) является универсальной накрывающей группы RР². Другими словами, группа RР² представляет собой двулистное изображение группы SU(3).

В пользу того, что симметрия сильных взаимодействий соответствует симметрии группы RР², говорит и возможность представить проективную плоскость в виде так называемой поверхности Боя ([4] т.1, стр.134). Это односторонняя поверхность, состоящая из 3-х лепестков (рис.4 ) (данный рисунок получен с сайта http://en.wikipedia.org/).

 

Рис.4

 

Данная модель позволяет объяснить невылетание кварков чисто кинематическим образом, хотя она не исключает описание в виде взаимодействия с восемью векторными частицами (по числу независимых параметров группы RР²). Эти частицы (глюоны) можно рассматривать как материальные образования, из которых и построена поверхность Боя каждого адрона.

1.4. Слабое взаимодействие.

Слабое взаимодействие характеризуется последней из оставшихся непрерывных симметрий 3-х мерного действительного проективного пространства RР³, а именно - симметрией сферы S³. Группа преобразований сферы S³ в точности совпадает с группой SU(2), которая, согласно современным представлениям, и является группой симметрии слабого взаимодействия.

Данная интерпретация слабого взаимодействия делает понятным, почему только оно способно нарушать симметрию сильных взаимодействий. Суть этого процесса заключается в следующем. При одновременном участии сильных и слабых взаимодействий происходит наложение симметрии RР² и симметрии S³. В результате, частицы, входящие в состав поверхности Боя (кварки), могут совершать движение из лепестка в лепесток не только через центральное ядро, но и через пространство между лепестками, «заполненное» сферой S³. В процессе такого движения частица может не дойти до следующего лепестка, что приведет к разрушению исходного адрона.

1.5. Таким образом, предлагаемая проективная модель элементарных частиц предоставляет определенные геометрические образы для переносчиков всех четырех известных на данный момент взаимодействий. Другими словами, в рамках данной модели находят объяснение существование всех элементарных частиц-бозонов.

Более того, согласно данной модели, никаких других принципиально новых взаимодействий не должно быть. Соответствующие калибровочные симметрии просто не смогут «поместиться» внутри RР³ (возможное исключение указано в приложении №3).

Еще одним достоинством предлагаемой модели взаимодействий элементарных частиц является то, что все 4 взаимодействия рассматриваются на единой геометрической основе. При этом не вводится избыточной суперсимметрии, а для каждого взаимодействия устанавливается конкретный геометрический объект в рамках хорошо изученной геометрии, а именно, проективной геометрии трех измерений. По этой причине, в данной модели не возникает никаких «лишних» бозонов: в пространстве скоростей RР³ просто не существует других геометрических объектов, с которыми могли быть связаны эти «лишние» бозоны.

Другими словами, в данной модели предлагается единое геометрическое описание всех 4-х взаимодействий. Более того, в приложении №3 - также на единой геометрической основе - добавляется пятое взаимодействие, соответствующее открытой недавно "темной энергии".

2. Перейдем к рассмотрению механизма возникновения фермионов. Задача данного раздела – указать возможный путь объяснения того, что имеется всего 12 элементарных частиц-фермионов.

2.1. В основу предлагаемого механизма положен следующий математический факт: факторгруппа всех автоморфизмов Aut(О⁺(8)) по подгруппе внутренних автоморфизмов Int(О⁺(8)) изоморфна симметрической группе из 3-х элементов ([4] т.1, стр.236). Данная группа представляет собой множество трех одинаковых элементов, различающихся лишь порядковым номером. Естественно предположить, что данные элементы представляют собой 3 максимально тождественных сорта  частиц, которые изначально заполняют пространство СР³. Группу О⁺(8), по-видимому, можно отождествить с группой преобразований абсолюта О(4,С).

На второй стадии эволюции Вселенной каждый из указанных 3-х сортов частиц мог войти в состав абсолюта Q(СР³), а также остаться в пространстве СР³. В результате, возникло 2 класса частиц, в каждом из которых содержится по 3 семейства частиц. Частицы, которые вошли в абсолют, можно отождествить с «протолептонами», а частицы, оставшиеся в основной части пространства скоростей, - с «протокварками».

Третья стадия эволюции Вселенной привела к разделению «протокварков» на действительные, которые составили  пространство RР³, и комплексные, которые остаются не наблюдаемыми.

На следующей стадии (стадии Большого Взрыва), когда происходит пересечение действительного подпространства RР³, и абсолюта Q(СР³) пространства скоростей, каждое из указанных 3-х семейств делится на 2 вида. Частицы, составляющие абсолют Q(СР³), т.е. «протолептоны», разделяются на относительно тяжелые лептоны (электрон и 2 сорта мюонов), а также предельно легкие лептоны (3 сорта нейтрино). С другой стороны, частицы подпространства RР³, т.е. 3 семейства «протокварков», разделяются на верхний и нижний кварки, а также еще 2 подобные пары: странный и очарованный, а также прелестный и истинный кварки. В результате и получается, что количество элементарных частиц-фермионов имеет величину 3×2×2 = 12 частиц.

Заключительная стадия разделения, вероятно, происходила одновременно с разделением электрослабого взаимодействия на электромагнитное и слабое взаимодействия.

2.2. Рассмотрим кратко вопрос о структуре элементарных частиц.

2.2.1. Как было указано выше, лептоны имеют своим происхождением абсолют пространства скоростей. Имеется следующий изоморфизм абсолюта 3-х мерного комплексного проективного пространства Q(СP³) и собственной группы вращений 4-х мерного пространства, точками которого служат ориентированные торы  Т⁺(2) ~ О⁺(2) × О⁺(2) ([4] т.2,стр.54):

 

 S² × S²  ~ О⁺(4) / О⁺(2) × О⁺(2)               (8)

 

Данный изоморфизм позволяет рассматривать точки абсолюта пространства скоростей («протолептоны») в виде торов 4-х мерного пространства и наглядно представить пространственно-временные образы двух квантовых чисел лептонов, а именно заряда и спина:

1. элементарный  заряд – это одна из двух возможных ориентаций кольца тора (положительная или отрицательная), т.е. двух видов осевого вращения тора (отсутствие заряда означает, что тор превратился в бутылку Клейна).

 2. спин - это внутреннее вращение составляющих тело тора окружностей.

В данной модели минимальная величина спина, равная половине минимального момента орбитального вращения тора автоматически получается из условия согласования внутреннего и орбитального вращений. Только при условии, что в процессе внутреннего поворота окружностей тора на 180 градусов, точки тора за счет осевого вращения совершат оборот на 360 градусов, тор будет сохранять свою целостность.

2.2.2. Как уже было отмечено выше, адроны можно представлять в виде действительных проективных плоскостей RР² или, что эквивалентно, поверхностей Боя. Комбинируя шесть видов кварков в 3-х лепестках поверхностей Боя и вводя дополнительное условие, чтобы суммарный электрический заряд поверхности был целочисленным, можно получить весь наблюдаемый спектр адронов. В свою очередь, целочисленность заряда адронов является следствием совместного возникновения адронов и лептонов, а также условия электронейтральности мира.

Особенности интерпретации заряда, спина и других квантовых чисел адронов в рамках их представления поверхностями Боя будут исследованы позднее.

2.3. В заключение отмечу, что в математическом отношении предложенная теория элементарных частиц имеет немало точек пересечения с теорией суперсимметрии:

1. в качестве основной структуры рассматривается 8-мерное векторное пространство R⁸ (С⁴);

2. размерность пространства «внутренних» симметрий элементарных частиц (а именно, пространства скоростей СP³) имеет величину n=6, что соответствует 10-мерной теории элементарных частиц;

3. рассматриваются не только точечные элементы пространства, но также одномерные и двумерные объекты (RP¹ и RP²), которые можно отождествить с суперструнами и супермембранами.

Особенностью данной модели является то, что в ней указаны конкретные геометрические объекты, находящиеся внутри 6-ти мерного пространства скоростей, и соответствующие реальным физическим объектам. Эти объекты – действительное пространство скоростей RP³ и абсолют Q(СP³). Пересечение указанных объектов и позволяет практически однозначно определить все основные свойства элементарных частиц.

Благодаря указанной особенности, устраняется основной недостаток «слишком» симметричных моделей, а именно – наличие большого количества свободных параметров. В предлагаемой модели свободных параметры практически отсутствуют и количество элементарных частиц, вместе с их свойствами, получаются практически однозначно. Автор выражает надежду, что дальнейшее развитие модели позволит достичь этой однозначности в полной мере.

На момент создания сайта (январь 2006 года), автор сайта не располагает информацией о результатах в теории элементарных частиц, которые были получены в течение последних 15 лет. В ближайшие 2-3 года автор собирается восполнить этот пробел и дать количественную оценку всем указанным выше положениям. Возможно, что на этом пути удастся получить теоретическую связь между фундаментальными константами.

Результаты, которые будут получены после 17 января 2006 года, будут помещаться в разделе «Дополнение».

приложение  1               приложение 2              приложение 3   

 

главная  страница